Solución triángulo de Pascal

En la entrada anterior planteabamos un problema sobre el triángulo de Pascal. Dejamos aquí las soluciones.

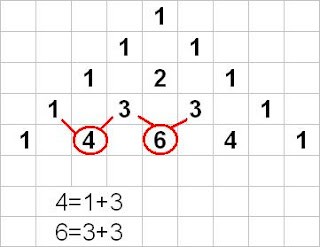
Proceso de formación de las filas.- Como puede observarse en la imagen, los elementos de cada fila se obtienen sumando los dos que tiene encima.

Luego ya sería sencillo obtener cualquier fila.
Ademas se puede observar que:
Todas las filas son simétricas.
Todas las filas empiezan por uno y terminan en uno.
La fila n-ésima está formada por (n+1) elementos.

a) El segundo número de la fila 125 es 124 (el segundo elemento de la fila n es siempre n-1)
b) La fila 103 tiene 103 elementos, como es un número impar, no todos los elementos se repiten, el central no.
c) Todos los número de la fila 5 suman 16 (2 elevado a 5-1=4)
Todos los número de la fila 7 suman 64(2 elevado a 7-1=6)
Todos los número de la fila 17 suman 2 elevado a 16=17-1
d) Todos los número de la fila n suman 2 elevado a n-1 (como puede verse en la figura de la izquierda)

e) Observamos los terceros elementos comenzando por la fila 5: 6, 10, 15, 21, 28, 36.... Luego parece que a cada elementos se le suma n-1, es decir a 6 (tercer elemento de la fila 5) se le suma 5-1=4 y sale 10. A 10 (tercer elemento de la fila 6) se le suma 6-1=5 y sale 15. A 15 (tercer elemento de la fila 7) se le suma 7-1=6 y sale 21. Luego el terner elemento de la fila n será la suma de la sucesión.